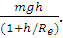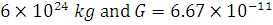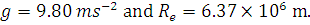Question
(i) A satellite is revolving in an orbit close to the earth’s surface. Taking the radius of the earth as 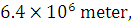 find the value of the orbital speed and the period of revolution of the satellite.
find the value of the orbital speed and the period of revolution of the satellite. 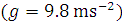
(ii) What is the relationship of this orbital speed to the velocity required to send a body from the earth’s surface into space, never to return?
Solution
Correct option is
84.6 minutes & 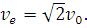
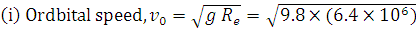
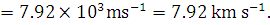
Period of revolution, 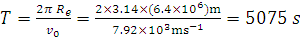
= 84.6 minutes.
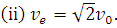
SIMILAR QUESTIONS
Q1
Calculate the gravitational field strength and the gravitational potential at the surface of the moon. The mass of the moon is 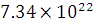 kg and its radius is
kg and its radius is 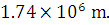
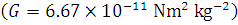 .
.
Q2
The intensity of gravitational field at a point situated at earth’s surface is 2.5 N/kg. Calculate the gravitational potential at that point. Given: radius of earth, 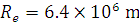 .
.
Q3
At a point above the surface of the earth, the gravitational potential is 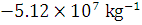 and the acceleration due to gravity is 6.4 ms–2. Assuming the mean radius of the earth to be 6400 km, calculate the height of this point above the earth’s surface.
and the acceleration due to gravity is 6.4 ms–2. Assuming the mean radius of the earth to be 6400 km, calculate the height of this point above the earth’s surface.
Q5
The radius of earth is 6400 km and mass is 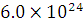 kg. What will be the gravitational potential energy of a body of 200 kg placed at a height of 600 km from the surface of the earth?
kg. What will be the gravitational potential energy of a body of 200 kg placed at a height of 600 km from the surface of the earth?
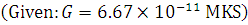 .
.
Q6
A body of mass m is moved from the surface of the earth to a height h (his not negligible in comparison to radius of earth Re). Prove that the increase in potential energy is 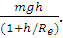
Q7
Calculate the velocity of projection of a particle so that the maximum height attained by the particle is 0.5 Re, where Re is radius of earth. The mass of earth is Me.
Q8
A satellite is revolving in a circular orbit at a distance of 2620 km from the surface of the earth. Calculate the orbital velocity and the period of revolution of the satellite. Radius of the earth = 6380 km, mass of the earth = 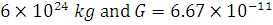 Nm2 kg–2.
Nm2 kg–2.
Q9
A satellite is revolving in a circular orbit at a distance of 3400 km. calculate the orbital velocity and the period of revolution of the satellite. Radius of the earth = 6400 km and g = 9.8 ms –2.
Q10
An artificial satellite revolving coplanar with the equator around the earth, appears stationary to an observer on the earth. Calculate the height of the satellite above the earth.
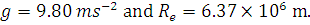

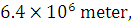 find the value of the orbital speed and the period of revolution of the satellite.
find the value of the orbital speed and the period of revolution of the satellite. 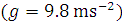
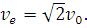
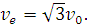
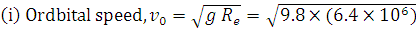
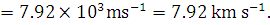
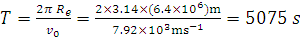
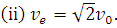
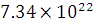 kg and its radius is
kg and its radius is 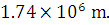
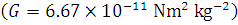 .
. 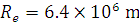
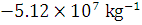
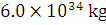
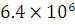
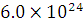 kg. What will be the gravitational potential energy of a body of 200 kg placed at a height of 600 km from the surface of the earth?
kg. What will be the gravitational potential energy of a body of 200 kg placed at a height of 600 km from the surface of the earth?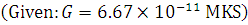 .
.