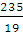Converting the given in-equations into equations, we obtain the following equations:
3x + 5y = 15, 5x + 2y = 10, x = 0 and y = 0
Region represented by 3x + 5y ≤ 15: The line 3x + 5y = 15 meets the coordinate axes at A1 (5, 0) and B1 (0, 3) respectively. Join these points to obtain the line 3x + 5y = 15. Clearly, (0, 0) satisfies the in-equation 3x + 5y≤ 15. So, the region containing the origin represents the solution set of the in-equation 3x + 5y ≤ 15.
Region represented by 5x + 2y ≤ 10: The line 5x + 2y = 10 meets the coordinate axes at A2 (2, 0) and B2 (0, 5) respectively. Join these points to obtain the line 5x + 2y = 10. Clearly, (0, 0) satisfies the in-equation 5x + 2y≤ 10. So, the region containing the origin represents the solution set of this in-equation.
Region represented by x ≥ 0 and y ≥ 0: Since every point in the first quadrant satisfies these in-equations. So, the first quadrant is the region represented by the in-equations x ≥ 0 and y ≥ 0.
The shaded region OA2 PB1 in fig. represents the common region of the above in-equations. This region is the feasible region of the given LPP.
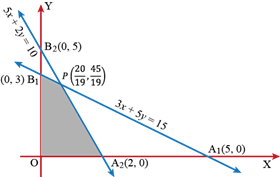
The co-ordinates of the vertices (corner-points) of the shaded feasible region are O (0, 0), A2 (2, 0), 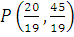 and B1 (0, 3).
and B1 (0, 3).
These points have been obtained by solving the equations of the corresponding intersecting lines, simultaneously.
The values of the objective function at these points are given in the following table.
|
Point (x, y) Value of the objective function
Z = 5x + 3y
|
|
O (0, 0) Z = 5 × 0 + 3 × 0 = 0
|
|
A2 (2, 0) Z = 5 × 2 + 3 × 0 = 10
|
|
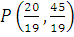 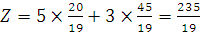
|
|
B1 (0, 3) Z = 5 × 0 + 3 × 3 = 9
|
Clearly, Z is maximum at 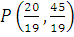 . Hence,
. Hence, 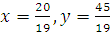 is the optimal solution of the given LPP. The optimal value of Z is
is the optimal solution of the given LPP. The optimal value of Z is