Question
In an ore containing uranium, the ratio of 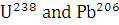 nuclei is 3. Calculate the age of the ore, assuming that all the lead present in the ore is the final stable product of
nuclei is 3. Calculate the age of the ore, assuming that all the lead present in the ore is the final stable product of 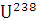 . Take the half-life of
. Take the half-life of 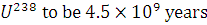 .
.
Solution
Correct option is

All the lead present in the ore is the final stable product of 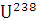 . It means that the number of nuclei of
. It means that the number of nuclei of  present is equal to the number of nuclei of
present is equal to the number of nuclei of 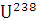 decayed.
decayed.
Let the number nuclei of  be N. Then, the number of nuclei of
be N. Then, the number of nuclei of 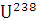 present in the ore is 3N.
present in the ore is 3N.


 .
.


 .
.
If, in a radioactive substance, initially and after the time t, the number of nuclei be N0 and N’ respectively, then







 .
.
SIMILAR QUESTIONS
Q2
The disintegration rate of a certain radioactive sample at any instant is 4750 disintegrations per minute. 5 minute after, the rate becomes 2700 disintegrations per minute. Calculate the half-life of the sample.  .
.
Q3
At a given instant are 25% undecayed radioactive nuclei in a sample. After 10 seconds, the number of undecayed nuclei reduces to 12.5%. Calculate the time in which the number of undecayed nuclei will further reduce to 6.25% of the reduced number.
Q4
The normal activity of a living mater containing radioactive carbon C14 is found to be 15 decays per minute per gram of carbon. An archaeological specimen shows an activity of 9 decays per minute per gram of carbon. Estimate the age of the specimen. The half-life of C14 is 5730 years.
Q5
A radioactivity sample contains 2.2 mg of pure 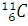 which has half-life period of 1224 seconds. Calculate the number of atoms present initially.
which has half-life period of 1224 seconds. Calculate the number of atoms present initially.
Q6
A small quantity of solution containing 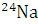 radionuclide (half-life 15 hours) of activity 1.0 microcurie is injected into the blood of a person. A sample of the blood of volume 1 cm3 taken after 5 hours show an activity of 296 disintegrations per minute. Determine the total volume of blood in the body of the person.
radionuclide (half-life 15 hours) of activity 1.0 microcurie is injected into the blood of a person. A sample of the blood of volume 1 cm3 taken after 5 hours show an activity of 296 disintegrations per minute. Determine the total volume of blood in the body of the person.
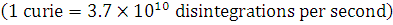 .
.
Q7
The isotopes 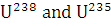 occur in nature in the ratio 140 : 1. Assuming that at the time of earth’s formation they were present in equal ratio, make an estimation of the age of the earth. The half-lives of
occur in nature in the ratio 140 : 1. Assuming that at the time of earth’s formation they were present in equal ratio, make an estimation of the age of the earth. The half-lives of 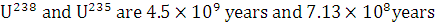 respectively.
respectively.
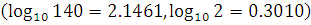
Q8
A radioactive isotope X has a half-life of 3 seconds. At t = 0 second, a given sample of this isotope X contains 8000 atoms. Calculate the number of decays per second in the sample at t = t1 second.
Q9
A radioactive element of atomic weight 99 has a half-life of 6 hours. Find the activity in a solution containing 1 gram of the element in the beginning. The Avogadro’s number is 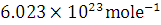 .
.

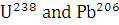
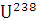
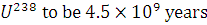









 .
. 






 .
.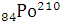
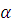
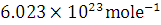
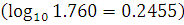
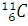
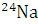
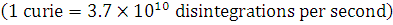 .
.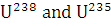
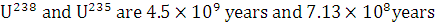
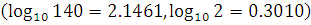
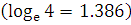 .
.