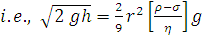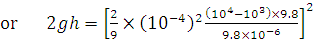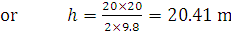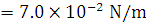Question
A spherical ball of radius 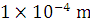 and 104 kg/m3 falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h. The viscosity of water is
and 104 kg/m3 falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h. The viscosity of water is 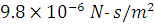 .
.
Solution
Correct option is
20.41 m
After falling a height h the velocity of the ball will become 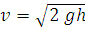 . As after entering the water this velocity does not change, this velocity is equal to terminal velocity,
. As after entering the water this velocity does not change, this velocity is equal to terminal velocity,
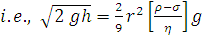
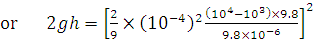
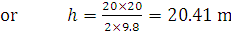
SIMILAR QUESTIONS
Q1
Two capillary tubes of diameters 5.0 mm and 4.0 mm are held vertically inside water one by one. How much high the water will rise in each tube? (g = 9.8 N kg–1, surface tension of water 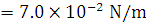 )
)
Q2
Water rises in a capillary tube to a height 2.0 cm. In an another capillary whose radius is one-third of it, how much the water will rise? If the first capillary is inclined at an angle of 60o with the vertical then what will be the position of water in the tube?
Q3
A cylindrical tank 1 m in radius rests on a platform 5 m high. Initially the tank is filled with water upto a height of 5 m. a plug whose area is 10–4 m2is removed from an orifice on the side of the tank at the bottom. Calculate time taken to empty the tank to half its original value.
Q4
A boat of area 10 m2 floating on the surface of a river is made to move horizontally with a speed of 2 m/s by applying a tangential force. If the river is 1 m deep and the water in contact with the bed is stationary, find the tangential force needed to keep the boat moving with same velocity. Viscosity of water is 0.01 poise.
Q5
The velocity of water in a river is 18 km/hr at the surface. If the river is 5 m deep, find the shearing stress between the horizontal layers of water. The viscosity of water is 10–3 poiseuille.
Q6
The velocity of a small ball of mass m and density d1 when droped in a container filled with glycerine becomes constant after some time. What is the viscous force acting on the ball if density of glycerine is d2?
Q7
Find the velocity of glycerine (having density 1.3 g/cc) if a steel ball of 2 mm radius (density = 8 g/cc) acquires a terminal velocity of 4 cm/s in falling freely in the tank of glycerine.
Q8
An area bubble of radius 1mm is allowed to rise through a long cylindrical column of a viscous liquid of radius 5 cm and travels at a steady rate of 2.1 cm per sec. If the density of the liquid is 1.47 g per cc, find its velocity. Assume g = 980 cm/sec2 and neglect the density of air.
Q9
Two equal drops of water are falling through air with a steady velocity v. If the drops coalesced, what will be the new velocity.
Q10
Water flows through a capillary tube of radius r and length l at a rate of 40 ml per second, when connected to a pressure difference of h cm of water. Another tube of the same length but radius r/2 is connected in series with this tube and the combination is connected to the same pressure head. Calculate the pressure difference across each tube and the rate of flow of water through the combination.

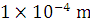
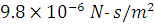
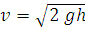 . As after entering the water this velocity does not change, this velocity is equal to terminal velocity,
. As after entering the water this velocity does not change, this velocity is equal to terminal velocity,