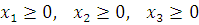A firm can produce three types of cloth, say C1, C2, C3. Three kinds of wool are required for it, say red wool, green wool and blue wool. One unit of length C1 needs 2 metres of red wool, 3 metres of blue wool; one unit of cloth C2 needs 3 metres of red wool, 2 metres of green wool and 2 metres of blue wool; and one unit of cloth C3 needs 5 metres of green wool and 4 metres of blue wool. The firm has only a stock of 16 metres of red wool, 20 metres of green wool and 30 metres of blue wool. It is assumed that the income obtained from one unit of length of cloth C1 is Rs. 6, of cloth C2 is Rs. 10 and of cloth C3 is Rs. 8. Formulate the problem as a linear programming problem to maximize the income.
Solution
Correct option is
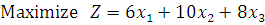
Subject to the constraints
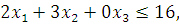
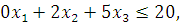
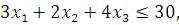
And, 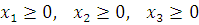
The given information can be put in the following tabular form:
|
|
Cloth C1 Cloth C2 Cloth C3
|
Total quantity of wood available
|
|
Red Wool
Green Wool
Blue Wool
|
2 3 0
0 2 5
3 2 4
|
16
20
30
|
|
Income(Rs.)
|
6 10 8
|
|
Let x1, x2, and x3 be the quantity produced in metres of the cloth of type C1, C2 and C3 respectively.
Since 2 metres of red wool are required for one metres of cloth C1 and x1metres of cloth C1 are produced, therefore 2x1 metres of red wool will be required for cloth C1. Similarly, cloth C2 requires 3x2 metres of red wool and cloth C3 does not require red wool. Thus, the total quantity of red wool required is 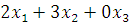
But the maximum available quantity of red wool is 16 metres.
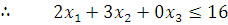
Similarly, the total quantities of green and blue wool required are
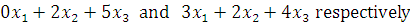 .
.
But the total quantities of green and blue wool available are 20 metres and 30 metres respectively.
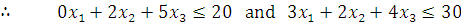
Also, we cannot produce negative quantities, therefore
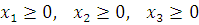
The total income is 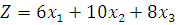
Hence, the linear programming problem for the given problem is
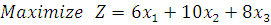
Subject to the constraints
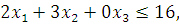
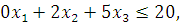
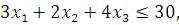
And,