The given data may be put in the following tabular form:
|
Food
|
Carbohydrate
|
Fat
|
Protein
|
Cost per unit
|
|
F1
F2
|
10
25
|
20
10
|
15
20
|
Rs 2
Rs 4
|
|
Minimum requirement
|
400
|
500
|
300
|
|
Suppose the diet contains x units of food F1 and y units of food F2.
Since one unit of food F1 costs Rs 2 and one unit of food F2 costs Rs 4. Therefore, total cost of x units of food F1 and y units of food F2 is Rs (2x+ 4y).
Let Z denote the total cost. Then,
Z = 2x + 4y.
Since each unit of food F1 contains 10 units of carbohydrate. Therefore, xunits of food F1 contain 10x units of carbohydrate. A unit of food F2contains 25 units of carbohydrate. So, y units of food F2 contain 25y units of carbohydrate.
Thus, x units of food F1 and y units of food F2 contain 10x + 25y units of carbohydrate.
But, the minimum requirement of carbohydrate is 400 units.
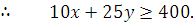
Similarly, the total amount of fat supplied by x units of Food F1 and yunits of food F2 is 20x + 10y and the minimum requirement is of 500 units.
∴ 20x + 10y ≥ 500.
Finally, the total amount of protein supplied by x units of food F1 and yunits of food F2 is 15x + 20y. But the minimum requirement of protein is of 300 units.
∴ 15x + 20y ≥ 300.
Clearly, x ≥ 0 and y ≥ 0.
Since we have to minimize the total cost Z = 2x + 4y.
Thus, the mathematical form of the given LPP is as follows:
Minimize Z = 2x + 4y
Subject to
10x + 25y ≥ 400
20x + 10y ≥ 500
15x + 20y ≥ 300
x, y ≥ 0.
