A Dietician Wishes To Mix Two Types Of Food In Such A Way That The Vitamin Contents Of The Mixture Contain At Least 8 Units Of Vitamin A and 10 Units Of Vitamin C. Food ‘I’ Contains 2 Units/kg Of Vitamin A and 1 Unit/kg Of Vitamin C while Food ‘II’ Contains 1 Unit/kg Of Vitamin A and 2 Units/kg Of Vitamin C. It Costs Rs 5.00 Per Kg To Purchase Food ‘I’ And Rs 7.00 Per Kg To Produce Food ‘II’. Determine The Minimum Cost To Such A Mixture. Formulate The Above As A LPP And Solve It. 

  1. Home
  2. JEE Main
  3. Maths
  4. Algebra
  5. Complex Numbers

Why Kaysons ?

Video lectures

Access over 500+ hours of video lectures 24*7, covering complete syllabus for JEE preparation.

Online Support

Practice over 30000+ questions starting from basic level to JEE advance level.

Live Doubt Clearing Session

Ask your doubts live everyday Join our live doubt clearing session conducted by our experts.

National Mock Tests

Give tests to analyze your progress and evaluate where you stand in terms of your JEE preparation.

Organized Learning

Proper planning to complete syllabus is the key to get a decent rank in JEE.

Test Series/Daily assignments

Give tests to analyze your progress and evaluate where you stand in terms of your JEE preparation.

SPEAK TO COUNSELLOR ? CLICK HERE

Download JEE Question paper & Solution Download JEE Important questions Download Complete syllabus of Maths, Physics, Chemistry

Question

A dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C while food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs 5.00 per kg to purchase food ‘I’ and Rs 7.00 per kg to produce food ‘II’. Determine the minimum cost to such a mixture. formulate the above as a LPP and solve it. 

Solution

Correct option is

2 kg of food ‘I’ & 4 kg of food ‘II’ and minimum cost will be Rs 38.00

 

Let the direction mix x kg of food ‘I’ with y kg of food ‘II’. Then, the mathematical model of the LPP is as follows:  

Minimize         Z = 5x + 7y

Subject to 2x + y ≥ 8      

                 x + 2y ≥ 10         

and,          x, y ≥ 0      

To solve this LPP graphically, we first convert the inequations into equations to obtain the following lines.   

       2x + y = 8, x + 2y = 10, x = 0, y = 0   

The line 2x + y = 8 meets the coordinates axes at A1 (4, 0) and B1 (0, 8). Join these points to obtain the line represented by 2x + y = 8. The region not containing the origin is represented by 2x + y ≥ 8.  

The line x + 2y = 10 meets the coordinates axes at A2 (10, 0) and B2 (0, 5). Join these points to obtain the line represented by x + 2y = 10. Clearly, O(0, 0) does not satisfy the inequation x + 2y ≥ 10. So, the region not containing the origin is represented by this inequation.

Clearly, x ≥ 0, y ≥ 0 represent the first quadrant. 

Thus, the shaded region in fig. is the feasible region of the LLP. The coordinates of the corner-points of this region are A­2 (10, 0), P (2, 4) andB1 (0, 8). 

                                                                

 

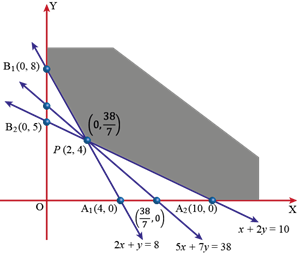
The point P (2, 4) is obtained by solving 2x + y = 8 and x + 2y = 10 simultaneously. The values of the objective function Z = 5x + 7y at the corner points of the feasible region are given in the following table:   

Point (x, y)

Value of the objective function

      Z = 5x + 7y

A2 (10, 0)

P (2, 4)

B1 (0, 8)

Z = 5 × 10 + 7 × 0 = 50

Z = 5 × 2 + 7 × 4 = 38

Z = 5 × 0 + 7 × 8 = 56   

Clearly, Z is minimum at x = 2 and y = 4. The minimum value of Z is 38. We observe that open half plane represented by 5x + 7y < 38 does not have points in common with the feasible region. So, Z has minimum value equal to 38 at x = 2 and y = 4.  

Hence, the optimal mixing strategy for the dietician will be mix 2 kg of food ‘I’ and 4 kg of food ‘II’. In this case, his cost will be minimum and the minimum cost will be Rs 38.00.   

Download JEE Question paper & Solution Download JEE Important questions Download Complete syllabus of Maths, Physics, Chemistry

SIMILAR QUESTIONS

Q1

 

A firm manufactures two products, each of which must be processed through two departments, 1 and 2. The hourly requirements per unit for each product in each department, the weekly capacities in each department, selling price per unit, labour cost per unit, and raw material cost per unit are summarized as follows: 

 

Product A

Product B

Weekly capacity

Department 1

3

2

130

Department 2

4

6

260

Selling price per unit

Rs 25

Rs 30

 

Labour cost per unit

Rs 16

Rs 20

 

Raw material cost per unit

Rs 4

Rs 4

 

The problem is to determine the number of units of produce each product so as to maximize total contribution to profit. Formulate this as a LLP.
easy View solution
Q2

 

Solve the following LPP graphically:  

Maximize    Z  = 5x + 3y  

Subject to  

           3x + 5y ≤ 15  

           5x + 2y ≤ 10 

And,    x, y ≥ 0.
diffcult View solution
Q3

 

Solve the following LPP by graphical method: 

Minimize    Z = 20x + 10y  

Subject to   x + 2y ≤ 40

                   3x + y ≥ 30  

                   4x + 3y ≥ 60 

And,           x, y ≥ 0
diffcult View solution
Q4

 

Solve the following LPP graphically:

Minimize and Maximize Z = 5x + 2y  

Subject to –2x – 3y ≤ – 6  

                     x – 2y ≤ 2

                    3x + 2y ≤ 12  

                  –3x + 2y ≤ 3 

                     x, y ≥ 0
diffcult View solution
Q5

 

Solve the following LPP graphically:

Maximize and Minimize   Z = 3x + 5y  

Subject to   3x – 4y + 12 ≥ 0

                       2x – y + 2 ≥ 0 

                   2x + 3y – 12 ≥ 0 

                               0 ≤ x ≤ 4 

                                      y ≥ 2.
medium View solution
Q6

 

Solve the following linear programming problem graphically:

Maximize  Z = 50x + 15y  

Subject to

            5x + y ≤ 100

             x + y ≤ 60

             x, y ≥ 0.
diffcult View solution
Q7

 

Solve the following LPP graphically:  

Maximize   Z = 5x + 7y  

Subject to

              x + y ≤ 4

             3x + 8y ≤ 24  

            10x + 7y ≤ 35

            x, y ≥ 0  
medium View solution
Q8

Solve the following LPP graphically:  

Minimize Z = 3x + 5y     

Subject to  

         – 2x + y ≤ 4  

            x + y ≥ 3

           x – 2y ≤ 2   

           x, y ≥ 0
medium View solution
Q9

 

A house wife wishes to mix together two kinds of food, X and Y, in such a way that the mixture contains at least 10 units of vitamin A,12 units of vitamin B and 8 units of vitamin C.

The vitamin contents of one kg of food is given below:   

 

Vitamin A

Vitamin B

Vitamin C

Food X:

1

2

3

Food Y:

2

2

1

One kg of food X costs Rs 6 and one kg of food Y costs Rs 10. Find the least cost of the mixture which will produce the diet.
diffcult View solution
Q10

Every gram of wheat provides 0.1 gm of proteins and 0.25 gm of carbohydrates. The corresponding values of rice are 0.05 gm and 0.5 gm respectively. Wheat costs Rs. 4 per kg and rice Rs. 6. The minimum daily requirements of proteins and carbohydrates for an average child are 50 gms and 200 gms respectively. In what quantities should wheat and rice be mixed in the daily diet to provide minimum daily requirements of proteins and carbohydrates at minimum cost.    
medium View solution