Every gram of wheat provides 0.1 gm of proteins and 0.25 gm of carbohydrates. The corresponding values of rice are 0.05 gm and 0.5 gm respectively. Wheat costs Rs. 4 per kg and rice Rs. 6. The minimum daily requirements of proteins and carbohydrates for an average child are 50 gms and 200 gms respectively. In what quantities should wheat and rice be mixed in the daily diet to provide minimum daily requirements of proteins and carbohydrates at minimum cost.

Question

Kaysons Education · Accepted Answer

Suppose x gms of wheat and y grams of rice and mixed in the daily diet. Since every gram of wheat provides 0.1 gm of proteins and every gram of rice gives 0.05 gm of proteins. Therefore, x gms of wheat and y grams of rice will provide 0.1x + 0.05y gms of proteins. But the minimum daily requirement of proteins is of 50 gms.

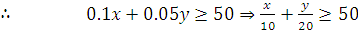
Similarly, x gms of wheat and y gms of rice will provide 0.25x + 0.5y gms of carbohydrates and the minimum daily requirement of carbohydrates is of 200 gms.

Since the quantities of wheat and rice cannot be negative. Therefore,

x ≥ 0, y ≥ 0

It is given that wheat costs Rs 4 per kg and rice Rs 6 per kg. So, x gms of wheat and y gms of rice will cost Rs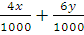

Hence, the given linear programming problem is

Minimize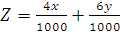

Subject to the constraints

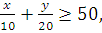
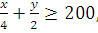
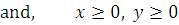
The solution set of the linear constraints is shaded in fig. The vertices of the shaded region are A₂ (800, 0), P (400, 200) and B₁ (0, 1000).

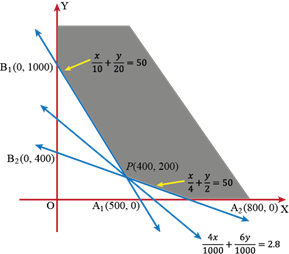
The values of the objective function at these points are given in the following table.

Point (x₁, x₂)

Value of objective function

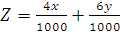
A₂ (800, 0)

P (400, 200)

B₁ (0, 1000)

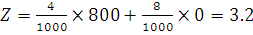
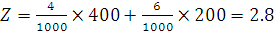
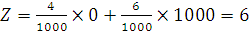
Clearly, Z is minimum for x = 400, y = 200 and the minimum value of Z is 2.8.

We observe that the open half plane represented by 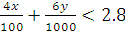does not have points is common with the feasible region. So, Z has minimum value 2.8 at x = 400 and y = 200.

Hence the diet cost in minimum when x = 400 and y = 200. The minimum diet cost is Rs 2.8.

	Vitamin A	Vitamin B	Vitamin C
Food X:	1	2	3
Food Y:	2	2	1

Why Kaysons ?

Video lectures

Online Support

Live Doubt Clearing Session

National Mock Tests

Organized Learning

Test Series/Daily assignments

SPEAK TO COUNSELLOR ? CLICK HERE

Question

Solution

SIMILAR QUESTIONS