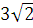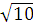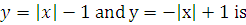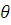Why Kaysons ?
Video lectures
Access over 500+ hours of video lectures 24*7, covering complete syllabus for JEE preparation.
Online Support
Practice over 30000+ questions starting from basic level to JEE advance level.
Live Doubt Clearing Session
Ask your doubts live everyday Join our live doubt clearing session conducted by our experts.
National Mock Tests
Give tests to analyze your progress and evaluate where you stand in terms of your JEE preparation.
Organized Learning
Proper planning to complete syllabus is the key to get a decent rank in JEE.
Test Series/Daily assignments
Give tests to analyze your progress and evaluate where you stand in terms of your JEE preparation.