An oil company requires 12,000, 20,000 and 15,000 barrels of high-grade, medium grade and low grade oil, respectively. Refinery A produces 100, 300 and 200 barrels per day of high-grade, medium-grade and low-grade oil, respectively, while refinery B produces 200, 400 and 100 barrels per day of high-grade, medium-grade and low-grade oil, respectively. If refinery A costs Rs 400 per day and refinery B costs Rs 300 per day to operate, how many days should each be run to minimize costs while satisfying requirements.
Solution
Correct option is
Machine A should run for 60 days & machine Bshould run for 30
The given data may be put in the following tabular form:
|
Refinery
|
High-grade Medium-grade Low-grade
|
Cost per day
|
|
A
B
|
100 300 200
200 400 100
|
Rs 400
Rs 300
|
|
Minimum requirement
|
12,000 20,000 15,000
|
|
Suppose refineries A and B should run for x and y days respectively to minimize the total cost.
The mathematical form of the above LPP is
Minimize Z = 400x + 300y
Subject to
100x + 200y ≥ 12000
300x + 400y ≥ 20,000
200x + 100y ≥ 15000
and, x, y ≥ 0
The feasible region of the above LPP is represented by the shaded region in fig.
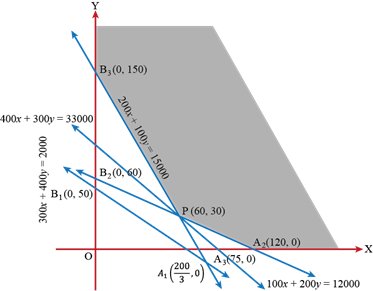
The corner points of the feasible region are A2 (120, 0), P (60, 30) and B3(0, 150). The value of the objective function at these points are given in the following table:
|
Point (x, y)
|
Value of the objective function
Z = 400x + 300y
|
|
A2 (120, 0)
P (60, 30)
B3 (0, 150)
|
Z = 400 × 120 + 300 × 0 = 48000
Z = 400 × 60 + 300 × 30 = 33000
Z = 400 × 0 + 300 × 150 = 45000
|
Clearly, Z is minimum when x = 60, y = 30. The feasible region is unbounded. So, we find the half-plane represented by 400x + 300y < 33000. Clearly, the half-plane does not have points common with the feasible region. So, Z is minimum at x = 60, y = 30.
Hence, the machine A should run for 60 days and the machine B should run for 30 days to minimize the cost while satisfying the constraints.

