Why Kaysons ?
Video lectures
Access over 500+ hours of video lectures 24*7, covering complete syllabus for JEE preparation.
Online Support
Practice over 30000+ questions starting from basic level to JEE advance level.
Live Doubt Clearing Session
Ask your doubts live everyday Join our live doubt clearing session conducted by our experts.
National Mock Tests
Give tests to analyze your progress and evaluate where you stand in terms of your JEE preparation.
Organized Learning
Proper planning to complete syllabus is the key to get a decent rank in JEE.
Test Series/Daily assignments
Give tests to analyze your progress and evaluate where you stand in terms of your JEE preparation.
SPEAK TO COUNSELLOR ? CLICK HERE

JEE Maths Overview & Analysis
Maths:
Maths is a subject that requires a lot of practice owing to various formulas and questions that can be made out of its variations and derivations. A certain sense of trend needs to be established before going into the examination to be able to swiftly solve the questions within the limited time frame. Among all its units, Algebra takes up a huge 33% followed by Calculus with 31%.Vectors, 3D Geometry and Coordinate Geometry further contribute 26% together.
Some of the most important chapters are: Definite Integration, Differential Equation, Application of Derivatives, Vectors, 3D Coordinate Geometry, Sequence & Series, Matrices & Determinants, Probability, and Straight Line.
Units Covered in JEE Maths
Integral Calculus
Differential Calculus
Vectors & 3D Geometry
Algebra
Coordinate Geometry
Trigonometry
Mathematical Reasoning
JEE Maths analysis 2010 to 2020
The graph below shows the mark distribution of the subjects:
.png)
JEE Maths marks distribution from 2010 to 2020
The chart below shows the mark distribution of the subjects across the years:
List of Best books for Jee Maths
- 1 N Awasthi - Physical Chemistry
- P Bahadur - Concept of Physical Chemistry for JEE Main &Advanced
- R.K Gupta - Arihant's Practice Book Chemistry for JEE Main And Advanced
- MS Chauhan - Elementary problems in Organic Chemistry
- O.P. Tandon - Physical Chemistry
- O.P. Tandon - Organic Chemistry
- P.W.Atkins - Physical Chemistry
JEE Math Syllabus 2021
- Integral as an anti-derivative, Fundamental Integrals involving algebraic, trigonometric, and exponential and logarithms functions.
- Integrations by substitution, by parts and by partial functions.
- Integration using trigonometric identities.
- Evaluation of simple integrals of the type
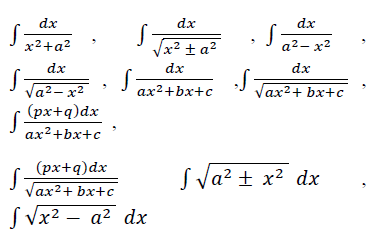
- Integral as limit of a sum.
- The fundamental theorem of calculus, properties of definite integrals.
- Evaluation of definite integrals, determining areas of the regions bounded by simple curves in standard form.
- Ordinary differential equations, their order and degree, the formation of differential equations, solution of differential equation by the method of separation of variables, solution of a homogeneous and linear differential equation of the type 𝑑𝑦/𝑑𝑥 + 𝑝(𝑥)𝑦 = 𝑞(𝑥)
- Sets and their representation: Union, intersection and complement of sets and their algebraic properties; Power set;
- Relation, Type of relations, equivalence relations
- Functions; one-one, into and onto functions, the composition of functions.
- Real – valued functions, algebra of functions, polynomials, rational, trigonometric, logarithmic and exponential functions, inverse function.
- Graphs of simple functions. Limits, continuity and differentiability.
- Differentiation of the sum, difference, product and quotient of two functions.
- Differentiation of trigonometric, inverse trigonometric, logarithmic, exponential, composite and implicit functions
- Derivatives of order up to two, Rolle’s and Lagrange's Mean value Theorems
- Applications of derivatives: Rate of change of quantities, monotonic- Increasing and decreasing functions, Maxima and minima of functions of one variable, tangents and normal.
- Coordinates of a point in space, the distance between two points, section formula, directions ratios and direction cosines, the angle between two intersecting lines.
- Skew lines, the shortest distance between them and its equation.
- Equations of a line and a plane in different forms, the intersection of a line and a plane, coplanar lines.
- Vectors and scalars, the addition of vectors, components of a vector in two dimensions and three-dimensional space, scalar and vector products, scalar and vector triple products.
- Complex numbers as ordered pairs of reals, Representation of complex numbers in the form a + ib and their representation in a plane, Argand diagram, algebra of complex number, modulus and argument (or amplitude) of a complex number, square root of a complex number, triangle inequality
- Quadratic equations in real and complex number system and their solutions Relations between roots and co- efficient, nature of roots, the formation of quadratic equations with given roots.
- Matrices, algebra of matrices, type of matrices, determinants and matrices of order two and three, properties of determinants, evaluation of determinants, area of triangles using determinants, Adjoint and evaluation of inverse of a square matrix using determinants and elementary transformations, Test of consistency and solution of simultaneous linear equations in two or three variables using determinants and matrices.
- The fundamental principle of counting, permutation as an arrangement and combination as section, Meaning of P (n,r) and C (n,r), simple applications.
- Binomial theorem for a positive integral index, general term and middle term, properties of Binomial coefficients and simple applications.
- Arithmetic and Geometric progressions, insertion of arithmetic, geometric means between two given numbers, Relation between A.M and G.M sum up to n terms of special series; Sn, Sn2, Sn3. Arithmetico-Geometric progression.
- Measures of discretion; calculation of mean, median, mode of grouped and ungrouped data calculation of standard deviation, variance and mean deviation for grouped and ungrouped data.
- Probability: Probability of an event, addition and multiplication theorems of probability, Baye's theorem, probability distribution of a random variate, Bernoulli trials and binomial distribution.
- Cartesian system of rectangular co- ordinates in a plane, distance formula, sections formula, locus and its equation, translation of axes, the slope of a line, parallel and perpendicular lines, intercepts of a line on the co-ordinate axis.
- Straight line: Various forms of equations of a line, intersection of lines, angles between two lines, conditions for concurrence of three lines, the distance of a point form a line, equations of internal and external by sectors of angles between two lines co- ordinate of the centroid, orthocentre and circumcentre of a triangle, equation of the family of lines passing through the point of intersection of two lines.
- Circle, conic sections: A standard form of equations of a circle, the general form of the equation of a circle, its radius and central, equation of a circle when the endpoints of a diameter are given, points of intersection of a line and a circle with the centre at the origin and condition for a line to be tangent to a circle, equation of the tangent, sections of conics, equations of conic sections (parabola, ellipse and hyperbola) in standard forms, condition for Y = mx +c to be a tangent and point (s) of tangency.
- Trigonometrical identities and equations, trigonometrical functions, inverse trigonometrical functions and their properties, heights and distance
- Statement logical operations and, or, implies, implied by, if and only if, understanding of tautology, contradiction, converse and contrapositive.
- Principle of Mathematical Induction and its simple applications.
Q. How can I study Math for IIT JEE?
Studying Maths for IIT JEE is not a very tough thing if you know what to do. You can start studying NCERT books because they will help you prepare for your JEE exams. However, for IIT you need to really practice hard, refer to many books, watch video lectures with Kaysons Education and enroll at a reputed institute like Kaysons to excel in IIT JEE Maths.
Q. Is JEE Maths difficult?
JEE Maths is only difficult if you don’t prepare or you don’t practice or opt for a trustworthy coaching center to guide you like Kaysons Education. However, if you face the problems, clear all the doubts, and keep yourself updated in terms of knowledge, JEE Maths is not difficult to score in!
Q. How can I score good marks in JEE maths?
You need to practice maths regularly, look for good books for studying, refer to interactive video lessons, opt for doubt-clearing sessions and go as per the course demands in order to ace your JEE Maths examinations. Most importantly, you shouldn't worry because Kaysons Education is there to help you! Try their Youtube channel here: https://youtube.com/kaysonsedu
Q. How can I get 70+ in JEE Maths?
If you want to score above 70+ in JEE Maths, first of all, you need to know all the formulas by heart, refer to NCERT books, devote at least an hour to Maths and go through the doubt clearing sessions and video lectures for Maths that Kaysons bring you. Acing your JEE Maths will not be a big deal this way!
Q. Can I skip maths in JEE Mains?
You can wish Maths can be skipped, but that cannot be done in JEE Mains. It is an essential subject and you can score high grades in Maths by reaching out to Kaysons for important insights!
Q. How can I get full marks in JEE maths?
Maths is a very scoring subject that can lift your grades big time. Devoting an hour to Maths and remembering all the formulae can be a good start to it. Now, if you cannot manage that or you want to enroll at a reputed institute, then contact Kaysons Education because they provide the best teachers and classes to excel in Maths.
